1. Introduction

Qubits are regarded by researchers as a new way to obtain bits for using them in computation. Quantum computing is based on quantum mechanics (a branch of physics), studying the behavior of subatomic particles such as electrons and photons. (Information Technology and Information Foundation, 2018) These studies are about obtaining quantum bit states or qubits.Nevertheless, qubits are extremely fragile and must be operated at temperatures near absolute zero, so they are susceptible to systemic failure. After more research on stabilizing qubits, rudimentary quantum computers appeared. Now, having laboratory prototypes bringing applications of “quantum information science”, such as quantum computing, quantum communications quantum sensing and quantum imaging, these quantum computers will be practical. (Information Technology and Information Foundation, 2018).

As a convention, Felix Bloch represents the bit states of a qubit on a sphere as polar coordinates. Its north pole is 0 (0 radians) bit and the south pole is 1 bit (π radians).

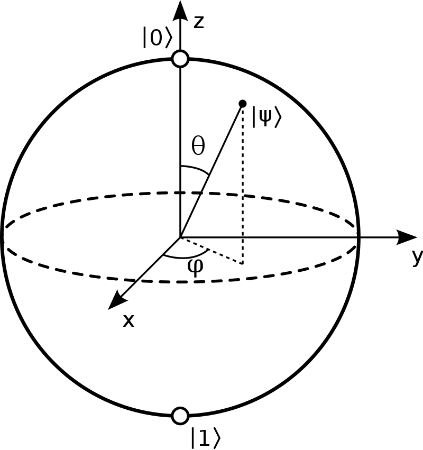
Figure 1. Representation of qubit states on a Bloch sphere (Source: Bloch, 1946)

The other points on the sphere’s surface are superpositions which helps us to obtain random values. Such a point belongs to a vector starting from sphere's center to its surface. These vectors take binary values, then written as matrices. According to Bloch, to vectors \(|0\rangle\) and \(|1\rangle\) correspond \(\begin{matrix}1 \\0\end{matrix}\) and respectively \(\begin{matrix}0 \\1\end{matrix}\) matrices.

A qubit returns combinations of two bits, given by the two angles on Bloch's sphere, θ and φ. (Shukla and Patel, 2018)

Particles used for obtaining qubits are:

• electrons, in which the electron movements have two levels considered: spin up and spin down.
• photons, in which the polarization of a single photon means the two states can be taken to be the vertical polarization and the horizontal polarization. (Bloch, 1946)
• other particles, for example ions.

More types of qubits were discovered:

• Superconducting qubits, in which Lu Yong, Bengtsson A. and Burnett J. explains that superconducting qubits are based on artificial atoms. Superconducting circuits are promising building blocks for creating quantum computers.

For example, Intel Labs developed Tangle Lake, a superconducting quantum processor. (Takahashi, 2020)

• Spin qubits, which function on the basis of the spin of a single electron in silicon, controlled by microwave pulses. On this basis, spin qubits are controlled by microwave pulses. (RIKEN Center for Emergent Matter Science, 2020)

2. Qubit Properties

There are four main properties of qubits, enabling new functionalities that researchers use for improving the digital signaling, therefore bringing new features in technology:

1) Superposition: a qubit has two states simultaneously for a duration. When its energy runs out, the qubit remains in a single state. Qubits can represent numerous possible combinations of 1 and 0 at the same time. (Giles, 2019) These are combinations of 0s and 1s. In Fig. 1, such a value has a vector, with its projections on xy and yz planes and the angles resulted θ and φ. (Bloch, 1946)

2) Entanglement: given a pair of qubits, when a qubit changes its state, the other one changes its state as well - they correlate. (Giles, 2019) One qubit’s state can be programmed to act according to another qubit's state.

3) Decoherence: qubits suffer influences from the environment, and this is why they are kept isolated. However, they are still vulnerable to noise that causes lots of computing errors. Smart quantum algorithms can compensate for some of these, and adding more qubits also helps. (Giles, 2019)

4) Quantum supremacy: the ability of a quantum computer to make mathematical calculations that can be demonstrated. (Giles, 2019)

3. Related Work

In order to secure the integrity and confidentiality of a message, as well as the authenticity of its origin, an encryption primitive and an authentication primitive must be combined with a key distribution primitive. (ETSI GS QKD 002 QKD Use Cases, 2010).

BB84 is the first QKD protocol, appeared in 1984, by Charles Bennett and Gilles Brassard. (Shukla and Patel, 2018) In the BB84 experiment, based on the photon transmission, on the source and destination equipments, many researchers found vulnerabilities allowing interferences. In this situation, an intruder finds vulnerabilities and uses them to create an attack framework. However, an error check can be performed on both equipments and compare the results. Then, solutions can be provided, using the differences resulted of each equipment's number of errors.  (Bruss, D. et al., 2007)

The two parties, Alice and Bob analyze a part of the raw data, then establish the parameters of the channel, such as its transmissivity and noise. Furthermore, post-processing data will be analyzed, and a private shared key will be extracted from the remaining data. This is a stage of error correction, which allows them to detect and eliminate errors. In this discussion, intruder's attacks are compared with the action of flipping a coin. A number of wanted coin tosses is memorized, for example how many head tosses. This number is attributed to the number of attacks. Fewer tosses mean a weak result. This is called a weak basis dependence. (S. Pirandola et al., 2019)

If an attack is weak basis dependent, then the difference between the bit error rate and the phase error rate is small and this demonstration can help with:

• security against arbitrary attacks that satisfy a particular criterion for weak basis dependence,
• and to derive a lower bound on the asymptotic key generation rate.

Bennett-Brassard (BB84) quantum key distribution protocol shows that both the source and the detector have vulnerable points. A solution regarding the asymptotic key generation rate against weakly basis-dependent eavesdropping attacks and the estimation of rate is applied in cases when: sources emit weak coherent states with random phases, detectors with basis-dependent efficiency, and misaligned sources and detectors. (Shukla and Patel, 2018)

Also, BB84 protocol solves symmetry issues.  Symmetry between bases is when the source and destination have the same number of bit errors and phase errors.  The intruder can get information about this symmetry.

Shor and Preskill proved the security of BB84 by relating it to an entanglement distillation protocol.

BB84 addresses to the eavesdropping problem and was tested against eavesdropping using the Photon Number Splitting (PNS) attack. Under a PNS attack, Eve identifies and blocks single-photon pulses from reaching Bob while extracting information from multiphoton signal pulses.  Then Eve resends the remaining fraction of the multiphoton signal pulse to Bob via a lossless channel. Therefore, Eve obtains a small fraction from the key, so she will repeat these steps. Eve will stay undetected during this attack because Bob cannot distinguish between signal loss caused by high attenuation in the quantum channel and loss introduced by Eve blocking pulses.  Eve must match the fraction of the total number of pulses blocked to ensure she emulates the loss expected from the original attenuated quantum channel. Then Eve ensures that the overall photon number distribution is not altered and detectable. (Shukla and Patel, 2018)

4. Quantum Key Distribution

Once quantum computers evolved, quantum transmission became available, therefore quantum key distribution gained importance. (Giles, 2019)

In a quantum transmission, combinations of secret and public key sharing can be possible. [6] The list of approved QKD technologies is currently targeted for an annex to the "QKD Module security specification" of work item WI 8 [i.28]. (ETSI GS QKD 002 QKD Use Cases.2010)

Several industrial players, both ETSI members and non-members invested in QKD R&D as part of projects under the European Union’s Framework Programs 6 and 7. (ETSI World Class Standards)

A generic “prepare and measure” QKD protocol can be divided in two main steps: quantum communication followed by classical postprocessing. During quantum communication the sender (Alice) encodes instances of a random classical variable α into non-orthogonal quantum states. These states are sent over a quantum channel (optical fiber, free-space link) controlled by the eavesdropper (Eve), who tries to steal the encoded information. The linearity of quantum mechanics forbids to perform perfect cloning, so that Eve can only get partial information while disturbing the quantum signals. At the output of the communication channel, the receiver (Bob) measures the incoming signals and obtains a random classical variable β. After a number of uses of the channel, Alice and Bob share raw data described by two correlated variables α and β.  The remote parties use part of the raw data to estimate the parameters of the channel, such as its transmissivity and noise. Depending on this information, they in fact perform a stage of error correction, which allows them to detect and eliminate errors, followed by a stage of privacy amplification that allows them to reduce Eve’s stolen information to a negligible amount. (ETSI GS QKD 002 QKD Use Cases.2010)

4.1 Message authentication

An important requirement in QKD is message authentication, which requires key distribution for both sender and receiver. Both parties verify message integrity and authenticity of the message with the help of key distribution schemes (ETSI GS QKD 002 QKD Use Cases, 2010).

According to ETSI GS QKD 002 QKD Use Cases, secret key distribution can be:

• on a given secure channel or
• using public key cryptography.

A given secure channel can be, for example, the trusted courier who carries a USB flash drive filled with a random bit sequence, or a digital channel that is secured with a previously distributed secret key.

Quantum key distribution, too, requires authentication of the parties to avoid man-in-the-middle attacks. As a solution, the transmission on a classical channel uses a message authentication primitive to guarantee message integrity (ETSI GS QKD 002 QKD Use Cases, 2010). The QKD primitive requires message authentication for the key exchange between the two peers. Message authentication is about message integrity (i.e. that a message was not altered during transmission) and the identity of the sender, which are common goals. One approach is the digital signature that uses asymmetric encryption. To the message is applied a hash function and it is signed with a private key before sending. The receiver verifies the integrity and authentication of the message with the help of a public key. (ETSI GS QKD 002 QKD Use Cases, 2010)

Another method is the Message Authentication Code MAC. Sender and receiver use the same key for encrypting and verifying the MAC value and require prior distribution of symmetrical keys. (ETSI GS QKD 002 QKD Use Cases, 2010). In QKD, a key is generated continuously and a small fraction of it can be used for authenticating the message. When a channel is in operation, a pre-distributed initial secret is necessary to authenticate the public channel before the first set of quantum keys will be available. An ideal option is to combine QKD with one-time pad encryption and Universal-2 hashing to form a secret and authentic communication system with an unprecedented level of theoretical security. (ETSI GS QKD 002 QKD Use Cases, 2010)

Key predistribution is about sending keys or key rings to a destination, as shown in Fig.2: (Dai and Xu, 2010)

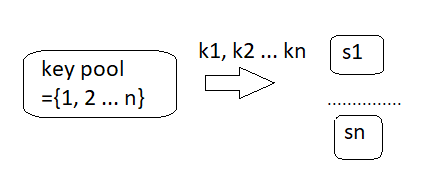
Figure 2. Key Pre-distribution

Fig. 2 shows that a key pre-distribution consists of a key pool that sends the keys to more network nodes.

The SECOQC project proves that a network combines QKD with an efficient implementation of universal hashing authentication and alternatively one-time pad or AES with frequent key change for payload encryption (ETSI GS QKD 002 QKD Use Cases, 2010). Shor and Preskill proved the security of BB84 by relating it to an entanglement distillation protocol (Shor and Preskill, 2000).

4.2 Photon polarization

The Figure 3 shows how a bit can be encoded in the polarization state of a photon in BB84. BB84 experiment shows that through polarization, bits are given values. So, the 0 bit is 0 degrees in the rectilinear bases and 45 degrees in the diagonal bases. Thus, a bit can be represented by polarizing the photon in either one of two bases. (Shukla and Patel, 2018)

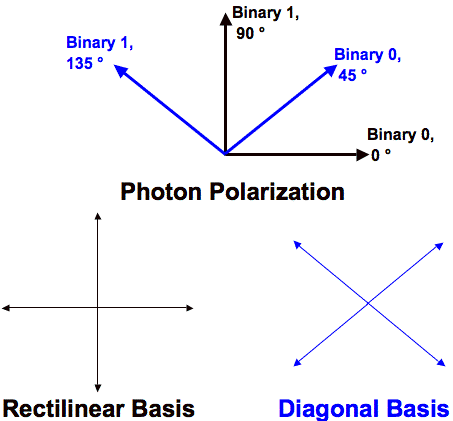
Figure 3. As seen on the Bloch sphere, each bit is encrypted with a rectilinear or diagonal basis, randomly chosen. (Source: Shukla and Patel, 2018)

Bit encryption involves assignation of symbols for each bit, as shown in Table 1. So, the bit values 0 and 1 and their corresponding symbols are listed as following:

Table 1. Qubit symbols for rectilinear and diagonal approaches (Source: Shukla and Patel, 2018)

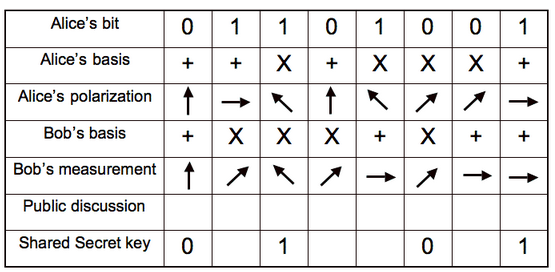
The key is 0101 sent by Alice to Bob on the quantum channel. Alice will randomly choose a basis (Table 1), rectilinear or diagonal, to encode each bit.

4.3 Architectures proposed

In Fig.4, communication takes place in a quantum channel, where Alice sends message to Bob. Also, Quantum-Safe Security Working Group presents the communication scheme and a diagram of the QKD architecture, in which:

1. Alice generates a random stream of classical bits and encodes them into a sequence of non-orthogonal quantum states of light, sent over the quantum channel
2. Bob performs some appropriate measurements leading him to share some classical data correlated with Alice’s bit stream upon reception of those quantum states
3. The classical channel tests these correlations

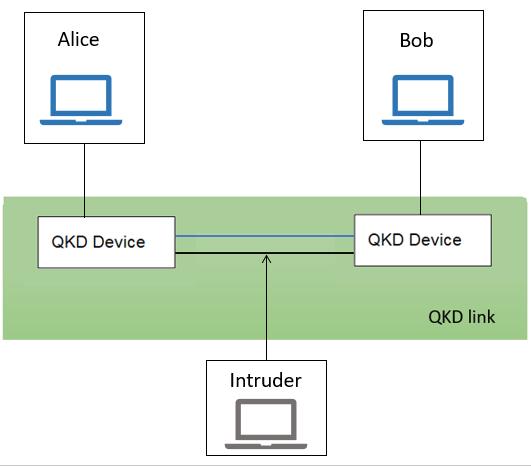
Figure 4. The intruder cannot break into the quantum channel (Source: Quantum-Safe Security Working Group)

In Figure 4, Alice and Bob send the message through the quantum encrypted medium (the blue link). The intruder can only see classic medium (black link), which is exposed. Sending and receiving of a message is done through QKD devices, which enable the quantum encryption link (blue link). (Quantum-Safe Security Working Group, 2018) Eve cannot see the stream sent by Alice. (Shukla and Patel, 2018) Such a channel is considered a secure channel because the messages transmitted come with previously distributed secret keys. (ETSI GS QKD 002 QKD Use Cases, 2010)

As an example, a QKD diagram which consists of a QKD channel and two communicating nodes having verification keys that send hashed messages to each other.

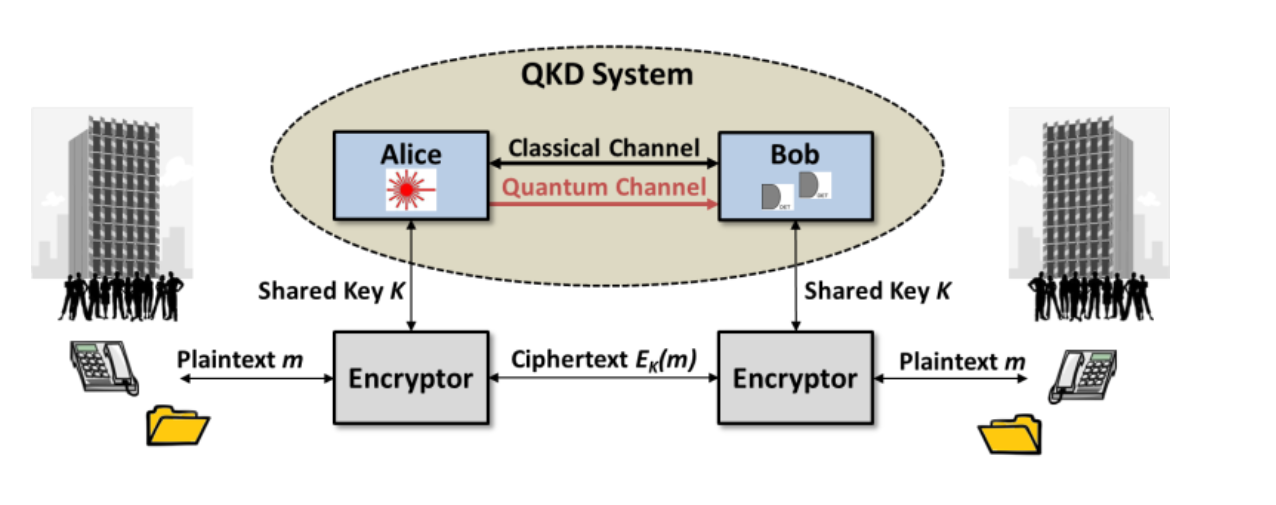
Figure 5. QKD System Context Diagram (Source: Mailloux, 2016)

In figure 5, the QKD system provides support for sharing s secret key, so sender (Alice) and receiver (Bob) share a secret key. Its applications include:

• sensitive data,
• voice,
• video communications. (Mailloux, 2016)

The QKD system can update a 256-bit AES key in a second, improving security. The adversary (Eve) cannot start cryptanalysis in such a short time. QKD system provides unlimited key material, for example one-time pad. In this situation, the keying material must be:

1. truly random,
2. never reused, and
3. if the message to be encrypted. (Mailloux, 2016)

In this situation, QKD can generate a shared cryptographic key, resulting a very resistant  one-time pad encryption configuration. (Mailloux, 2016)

5. Conclusion

At the beginning, during BB84 quantum connection testing for photon polarization, interferences were found, so error check verifications were included. These verifications are an important part of QKD authentication. A verification of received messages shows if an intruder tried to steal any message fragments. Throughout more research, highly secured transmissions were considered a possibility upon the SECOQC demonstrations.

In the future, quantum computers will improve the existing technology, so they might influence economy. Cyber intruders might take advantage on quantum devices, their processing level, our privacy could be in danger and economy may suffer from this.

6. References

Bloch, Felix. (1946). Nuclear Induction. Physical Review, 70(7–8), 460–474., https://doi.org/10.1103/PhysRev.70.460

Bruss, D., Erdélyi, G., Meyer, T., Riege, T., & Rothe, J. (2007). Quantum cryptography. ACM Computing Surveys, 39(2), 6. https://doi.org/10.1145/1242471.1242474

Takahashi, Dean. (2020). Intel and QuTech unveil Horse Ridge cryogenic control chip for quantum computing. Retrieved on 18.02.2020 from https://venturebeat.com/2020/02/18/intel-and-qutech-unveil-horse-ridge-cryogenic-control-chip-for-quantum-computing/

ETSI GS QKD 002. (2010). Quantum Key Distribution Use Cases. Retrieved on June 2010 from https://www.etsi.org/deliver/etsi_gs/qkd/001_099/002/01.01.01_60/gs_qkd002v010101p.pdf

ETSI World Class Standards. (2008) Quantum Key Distribution Architecture.Retrieved on 2008 from https://www.etsi.org/technologies/quantum-key-distribution

ETSI Quantum Key Distribution. Retrieved from  https://www.etsi.org/technologies/quantum-key-distribution

Information Technology and Information Foundation. (2019). TIF Technology Explainer: What Is Quantum Computing?. Retrieved on January 29, 2019 from  https://www.technologyreview.com/s/612844/what-is-quantum-computing/

Giles, M. (2019). Explainer: What is a quantum computer? Retrieved December 22, 2020, from https://www.technologyreview.com/2019/01/29/66141/what-is-quantum-computing/

Haitjema, Mart. (2007). A Survey of the Prominent Quantum Key Distribution Protocols. Retrieved on 2007 from https:/www.cse.wustl.edu/~jain/cse571-07/ftp/quantum/

Lu, Y., Bengtsson, A., Burnett, J. J., Wiegand, E., Suri, B., Krantz, P., … Delsing, P. (2019). Characterizing decoherence rates of a superconducting qubit by direct microwave scattering. Retrieved from http://arxiv.org/abs/1912.02124

Logan O. Mailloux, Dr. Michael R. Grimaila, Douglas D. Hodson, Colin V. McLaughlin and G.B. Baumgartner. 2016. Quantum Key Distribution: Boon or Bust? Published in Journal of Cyber Security and Information Systems, Volume: 4 Number: 2 - Basic Complexity

Shukla, M., & Patel, S. (2018). Prominent Security of the Quantum Key Distribution Protocol. International Journal of Science and Research, 8. https://doi.org/10.21275/ART20199396

Quantum-Safe Security Working Group.(2018). What is Quantum Key Distribution?. Retrieved on 2018 from https://www.etsi.org/images/files/ETSITechnologyLeaflets/QuantumKeyDistribution.pdf

Shor, P. W., & Preskill, J. (2000). Simple Proof of Security of the BB84 Quantum Key Distribution Protocol. Physical Review Letters, 85(2), 441–444. https://doi.org/10.1103/PhysRevLett.85.441

Pirandola, S., Andersen, U. L., Banchi, L., Berta, M., Bunandar, D., Colbeck, R., … Wallden, P. (2019). Advances in Quantum Cryptography. https://doi.org/10.1364/AOP.361502

RIKEN Center for Emergent Matter Science. (2020). Scientists measure electron spin qubit without demolishing it. Retrieved on 2.03.2020 from https://phys.org/news/2020-03-scientists-electron-qubit-demolishing.html

Dai, H., and Xu, H. (2010). Key Predistribution Approach in Wireless Sensor Networks Using LU Matrix. IEEE SENSORS JOURNAL, 10(8), 1399. https://doi.org/10.1109/JSEN.2009.2039130

Abbreviations

AES Advanced Encryption Standard

ETSI European Telecommunications Standards Institute

ICT Internet Communication Technology

BB84 Bennett-Brassard

MAC Message Authentication Code

QKD Quantum Key Distribution

R&D Research and Developments

PNS Photon Number Splitting

SECOQC Secure Communication based on Quantum cryptography